중위 표기식을 후위 표기식으로 변환 (괄호가 있는 경우)
e.g ) (2+10)/(9-6)
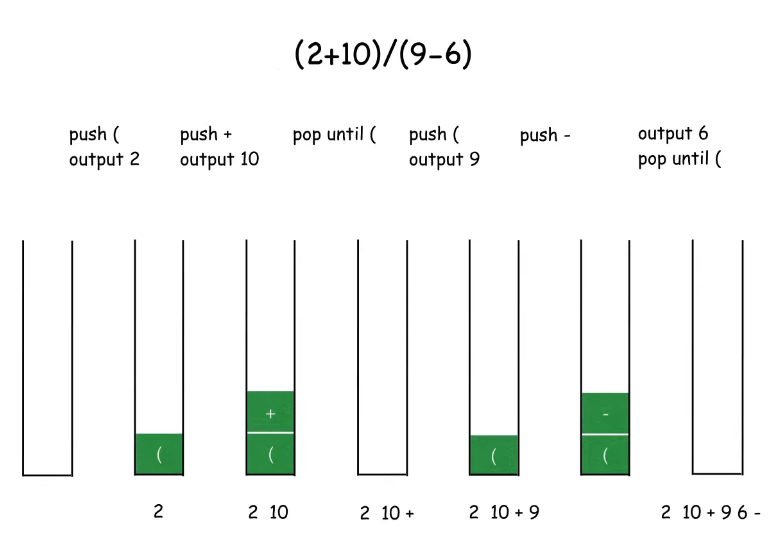
1. 여는 괄호는 무조건 스택에 push (Tip.이때 스택 내의 어떤 연산자도 pop 하지 않는다)
2. 어떤 연산자를 스택에 push할 때 스택의 top에 여는 괄호가 있으면 아무것도 pop하지 않고 push
3. 입력에 닫는 괄호가 나오면 스택에서 여는 괄호가 나올 때 까지 pop하여 출력한다.
4. 닫는 괄호는 스택에 push 하지 않는다. (stack의 여는 괄호도 pop 한다.)
# 괄호가 있는 중위 표기식을 후위 표기식으로 변환
# 입력 : 3 + ( ( 4 * 7 ) / 2 )
# 기대 출력 : [3, 4, 7, '*', 2, '/', '+']
OPERATORS = "+-*/()"
PRECEDENCE = [1,1,2,2,-1,-1] #여는 괄호의 우선순위를 -1로 정의
operator_stack = []
postfix = []
def is_operator(ch):
for i in range(len(OPERATORS)):
if (OPERATORS[i] == ch):
return i
return -1
def precedence(op): #우선 순위를 리턴해준다
return PRECEDENCE[is_operator(op)]
def process_op(op):
if (len(operator_stack) == 0 or op == '('): #여는 괄호는 그냥 스택에 push
operator_stack.append(op)
else:
top_op = operator_stack[-1]
if (precedence(op) > precedence(top_op)): #여는 괄호의 우선순위를 -1로 정의하여 가능
operator_stack.append(op)
else:
while(len(operator_stack) != 0 and precedence(op) <= precedence(top_op)):
operator_stack.pop() # 원래 pop을 하면 값을 받아야하지만 이전에 peek를 하여 따로 값을 받지는 않음
if top_op == '(': #op의 우선순위가 top_op 보다 낮거나 같은데 top_op가 여는 괄호이면 op는 닫는 괄호
break
postfix.append(top_op)
if (len(operator_stack) != 0):
top_op = operator_stack[-1] #stack이 비지 않았으면 top_op 값을 바꿔준다
if(op != ')'):
operator_stack.append(op)
return 0
def convert(infix):
token = infix.split(' ')
index = 0
while (index < len(token)):
if (token[index][0] >= '0' and token[index][0] <= '9'): # 가장 앞자리가 0에서 9 일 경우 정수
postfix.append(int(token[index]))
elif (token[index] in OPERATORS):
process_op(token[index])
else:
return 'Syntax Error'
index += 1
final_check = len(operator_stack)
while(final_check > 0):
op = operator_stack.pop()
if (op != '('): #괄호가 있으면 안됨
postfix.append(op)
final_check -= 1
else:
return 'Syntax Error'
return postfix
print(convert(input()))반응형
'CS(computer science) 지식 > 자료구조' 카테고리의 다른 글
| [자료구조] 큐(queue)의 이해 - python을 통한 실습 (6) (0) | 2022.11.23 |
|---|---|
| [자료구조] 스택(Stack)을 이용한 미로찾기 (5) (2) | 2022.11.23 |
| [자료구조] 스택(Stack)의 응용 중위표기식 -> 후위표기식 (4) (0) | 2022.11.11 |
| [자료구조] 스택(Stack)의 응용 후위표기식 - python을 통한 실습 (3) (0) | 2022.11.11 |
| [자료구조] 스택(Stack)의 이해 - python을 통한 실습 (2) (0) | 2022.11.09 |


